the complete question in the attached figure
let
x-----> distance AB
so
AC=2x
we know that
area of the figure=area of triangle+area of rectangle
area of the figure=90 ft²
step 1
find the area of triangle
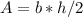
b=x
h=x
so

Area of triangle=x²/2 ft²
step 2
find the area of rectangle
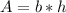
b=2x
h=x

area rectangle=2x²
step 3
find value of x
area of the figure=(x²/2)+2x²
area of the figure=90 ft²
90=(x²/2)+2x²-----> multiply by 2 both sides----> 180=x²+4x²
5x²=180-----> x²=36-----> x=6 ft
AC=2x-----> AC=2*6----> AC=12 ft
the answer isAC=12 ft