Question

Quadrilateral ABCD is a parallelogram. Determine the measure of _A.

OA) 96°
B) 78°
C) 52°
OD) 39°

Answer 1

The measure of angle A is: m∠A = 96

Therefore, option A is true.

Explanation:

Given

m∠C = 3x

m∠D = x+52

We know that the opposite angles of a parallelogram are also equal.

Determining m∠A

It is clear that A is the opposite angle of C.

i.e.

m∠A = m∠C

as m∠C = 3x

so m∠A = 3x

Determining m∠B

It is also clear that B is the opposite angle of D.

i.e.

m∠B = m∠D

as m∠D = x+52

so m∠B = x+52

We know that the sum of the angles of a parallelogram is 360°.

so

m∠A + m∠B + m∠C + m∠D = 360°

3x + (x+52) + 3x + (x+52) = 360°

Group like terms

`3x+x+3x+x+52+52=360^(\circ \:)`

`8x+104=360^(\circ \:)`

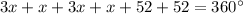
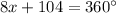
Subtract 104 on both sides

`8x+104-104=360^(\circ \:)-104`

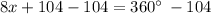
Simplify

`8x=360^(\circ \:)-104`

`8x=256`

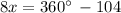
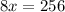
Divide both sides by 8

`(8x)/(8)=(256)/(8)`

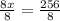
Simplify

`x=32`

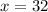
Thus,

The measure of the angle A is:

m∠A = 3x

substitute x = 32

m∠A = 3(32)

m∠A = 96

Hence, the measure of angle A is: m∠A = 96

Therefore, option A is true.