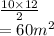Question

Does anybody know how to do question 2 please show working out

Answer 1

a)

`|CM|=(|BC|)/(2)\to|CM|=(10m)/(2)=5m`

b)

`h^2+5^2=13^2\\h^2+25=169\ \ \ |-25\\h^2=144\to h=√(144)\\h=12m`

c)

`A_\Delta=(|BC|h)/(2)\to A\Delta=(10\cdot12)/(2)=60\ m^2`

Answer 2

2a.
Since BC = 10m and M is the midpoint, we can find CM by : 10÷2 = 5m
So, CM = 5m

2b. Now, you have the base ( 5m) & hypotenuse (13m). Pythagoras' Theorem:


`c {}^(2) = {a}^(2) + {b}^(2)`
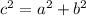
Where c is the hypotenuse, a & b are sides.


`{13}^(2) = {5}^(2) + b {}^(2) \\ {5}^(2) + {b}^(2) = 13 {}^(2) \\ {b}^(2) = 13 {}^(2) - {5}^(2) \\ b = √(144) \\ b = 12`
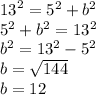
b here refers to the height.

2c.
Area of a right-angled triangle =

`(base * height)/(2)`
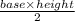
So,

`(10 * 12)/(2) \\ = 60 {m}^(2)`