Answer:
![x^{(9)/(7)} = \sqrt[7]{x^9}](https://img.qammunity.org/2022/formulas/mathematics/college/66kg27fs3e4xswm2wheetfsm8r4rm0hu89.png)
Explanation:
You can solve this by realising that the denominator of a fractional exponent can be expressed as the base of a radical.
Note also that the order does not matter. You could also express it as
![\sqrt[7]{x}^9](https://img.qammunity.org/2022/formulas/mathematics/college/f4xt9f3v7ju7iojquexaqcpdavtvsrh6kg.png)
The reason this works is that you're effectively breaking the exponent into fractions. The first answer is the equivalent of:
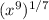
and the second would be:

In both cases, the exponents would be multiplied, giving the same result.