Answer:
The integers are 3 and 13
Explanation:
Let the integers are x and y.
Then from the given directions we can frame two equations.
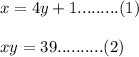
From equation 2, the value of x is
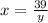
On substituting this value in equation 1, we get
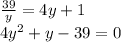
Applying the quadratic formula, we get
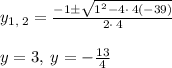
Among these two values, 3 is an integer.
Hence, y= 3
The value of x is x= 39/3 = 13
Therefore, the integers are 3 and 13