Question

the height h in feet of a projectile launched upward at a speed of 32 feet/ second from a height of 48 feet is given by the function : h(t) =16^2+32t +48. how long will it take the projectile to hit the ground?

Answer 1

If you are talking about parabolic motion, physics tells us that it goes up to a max and then drops down to the ground. This type of a parabola is a negative parabola, so I believe your formula should begin with a negative on that 16. Anyway, when you want to find how long it takes to hit the ground, you are looking for the values of t when the height is 0, since there is no height when an object is laying directly on the ground. Set the parabola equal to 0 and factor for the values of t.
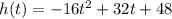
`h(t)=-16 t^(2)+32t+48`. Factor out a -16 to make things a bit easier:
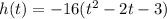
`h(t)=-16( t^(2)-2t-3)`. Of course -16 doesn't equal 0, so factor your quadratic to get the factors of (t-3)(t+1). There are 2 things in math that will never ever be negative and those are time and distance/length. Therefore, of our solutions t = 3 and t = -1, we would choose t = 3. In other words, it takes 3 seconds for the object to hit the ground when it is launched from a height of 48 feet at an initial upwards velocity of 32 feet/second.

Answer 2

Object will take 3 seconds to hit the ground.

Explanation:

We have been given a projectile motion which is a parabolic motion.

So In parabolic motion the object goes and then falls down.

So height is negative in that case because it is opposite direction.

`h(t)=-16t^2+32t+48`

`h(t)=16(-t^2+2t+3)`

`h(t)=16(-t^2+3t-t+3)`

`h(t)=16(-t(t-3)-1(t-3))`

`h(t)=-16(t+1)(t-3)` (1)

We will equate equation (1) to zero to get the value of t.

`-16\\eq0`

The
`(t+1)=0\rightarrow t=-1`

And
`(t-3)=0\rightarrow t=3`

Since time ca not be negative so t=3

Object will take 3 seconds to hit the ground.