We have to find the expected value for the PlayBall lottery.
The price of the ticket = $1
Prize amount = $250
If a player wins, he will be winning $249 as the price is not paid back along with the prize amount. He is spending $1, getting back $250, so the net amount he is getting back is $249.
Now we have to find the probability of winning and losing.
Number of letters from A to T = 20
Number of digits from 0 to 9 = 10
Probability of picking up the same letter that was picked on that day = 1/20
Probability of picking up the same number that was picked on that day = 1/10
Thus, the Probability of picking up the same letter and same number that was picked on that day =
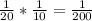
Thus, the probability of winning = 1/200
The probability of losing =

The expected value E for the PlayBall lottery will be:
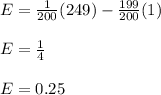 Thus, the option C gives the correct answer
Thus, the option C gives the correct answer