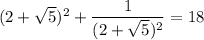Question

Exponential Equation WITHOUT CALCULATOR

Answer 1

Multiply both sides of the first equation by
`2^x`:


`2^x-2^(-x)=4\implies 2^(2x)-1=4\cdot2^x\implies 2^(2x)-4\cdot2^x-1=0`

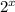
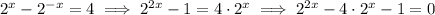
This is quadratic in
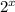
`2^x`; to make this clear, substitute
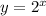
`y=2^x`. Then


`y^2-4y-1=0\implies y=2\pm\sqrt5`

One of these solutions for
`y` is negative. But, if
`x` is real, then
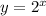
`y=2^x` is always supposed to be positive, so we can throw out the negative root, leaving
`y=2+\sqrt5`.

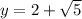
We actually don't have to solve for
`x` exactly. We can just rewrite the next two equations in terms of
`y`.



`2^(2x)+2^(-2x)=(2^x)^2+(2^(-x))^2=y^2+\frac1{y^2}`


`2^(3x)-2^(-3x)=y^3-\frac1{y^3}`


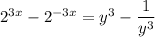
Since
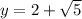
`y=2+\sqrt5`, we get


`(2+\sqrt5)^2+\frac1{(2+\sqrt5)^2}=18`


`(2+\sqrt5)^3-\frac1{(2+\sqrt5)^3}=76`