Question

`Let \: \: f(x)= [ ( \sin(x) )/(x) ] + [ ( 2\sin(2x) )/(x) ] + \: ... \: [ ( 10\sin(10x) )/(x) ] \\ \\ Where \: [y] \: is \: the \: largest \: integer \leqslant y ,\\ Find \: the \: value \: of \: \: \: x\xrightarrow[]{lim} 0\: \: \: f(x) \:`

Answer 1

Remark
When you take the limit of
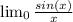
`\lim_( 0) (sin(x))/(x)` the odd result you get is 1. Later on you will be able to use calculus to show this. For now just take limits of sin(x)/x and make sure you are feeding radians into your calculator.

Now the only question is what is this thing doing?
If a is a constant in
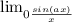
`\lim_{0 (sin(ax))/(x)` then the result = a.

So that's basically all you need to know to solve your problem.

Series
Each term in the series will be
a*(sin(ax)/x) = a * [sin(ax)/x] * 1 = a * a = a^2

The series will look like this.
1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 There is a way of summing this using n notation, but you could just as easily just add the results.

The formula for this series (if you want a sum) is n*(n+1)*(2n+1) / 6
n = 10
Sum = 10*(11)(21)/6
Sum = 385

Does adding it by hand bring up 385?