Question

Given: The coordinates of triangle PQR are P(0, 0), Q(2a, 0), and R(2b, 2c).

Prove: The line containing the midpoints of two sides of a triangle is parallel to the third side.

As part of the proof, find the midpoint of line PQ.

Answer 1

The answer you're looking for is (a, 0) Hope this helps!

Answer 2

Given: Coordinates of ΔPQR are P( 0 , 0 ) , Q( 2a , 0 ) and R( 2b , 2c )

To Proof: Line containing the midpoints x & Y of two sides PQ & PR of a triangle is parallel to the third side QR .i.e XY║QR

First We find Mid Point of side PQ and PR say X & Y respectively and then we find slope of line XY and QR. As if there slope is equal then they are parallel.

Formula of Mid point is given by

`Coordinates\,of\,Mid\,Point\,=\,((x_2+x_1)/(2),(y_2+y_1)/(2))`

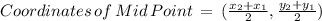
So, Coordinated of Mid Point of PQ , X =
`((2a+0)/(2),(0+0)/(2))`

=
`((2a)/(2),(0)/(2))`

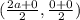
= ( a , 0 )

Coordinates of Mid Point of PR, Y =
`((2b+0)/(2),(2c+0)/(2))`

=
`((2b)/(2),(2c)/(2))`

= ( b , c )

Slope of a line is given by,

`Slope=(y_2-y_1)/(x_2-x_1)`

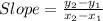
Slope of Line XY =
`(c-0)/(b-a)`

=
`(c)/(b-a)`

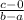
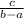
Slope of Line QR =
`(2c-0)/(2b-2a)`

=
`(2c)/(2(b-a))`

=
`(c)/(b-a)`

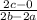
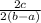
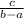
Since, Slope of XY = Slope of QR

⇒ XY is parallel to QR

Hence proved