You have to define the length in terms of the width or you have too many unknowns. L = w + 4. If the area is 60, the equation is 60 = w(w + 4). When you distribute that and set the quadratic equal to 0, then you have polynomial that you have to factor to find the dimensions. Here's your equation:
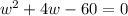
and when you factor that (I recommend using the quadratic formula) you get that w = 6 and w = -10. If you have 2 values for w, which one do you use? Always remember in math that there are 2 things that will NEVER EVER be negative and they are distance/length and time. So the value for w that you want is 6. That tells me that the width is 6 and the length is 6 + 4 which is 10 (not related at all to the -10 found in factoring. Purely coincidental. Promise)