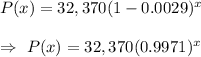Question

The 2000 U.S. Census reports the populations of Bozeman, Montana, as 27,509 and Butte, Montana, as 32,370. Since the 1990 census, Bozeman’s population has been increasing at approximately 1.96% per year. Butte’s population has been decreasing at approximately 0.29% per year. Assume that the growth and decay rates stay constant. Determine the exponential functions that model the populations of both cities.

Answer 1

Answer: Bozeman :
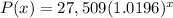`P(x)=27,509(1.0196)^x` , where x is number of years from 2000.

Butte:
`P(x)=32,370(0.9971)^x`, where x is number of years from 2000.

Explanation:

We know that the exponential growth function is given by :-

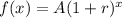`f(x)=A(1+r)^x`, where A is the initial value, r is the rate of increase and x is the time period.

Given: The population of Bozeman in 2000 = 27,509

The constant rate of increase = 1.96%=0.0196

Then, the exponential growth function that model the populations of Bozeman is given by :-

`P(x)=27,509(1+0.0196)^x\\\\\Rightarrow\ P(x)=27,509(1.0196)^x`

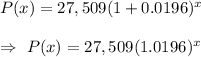
The population of Butte in 2000 = 32,370

The constant rate of decrease = 0.29% =0.0029

Then, the exponential growth function that model the populations of Butte is given by :-

`P(x)=32,370(1-0.0029)^x\\\\\Rightarrow\ P(x)=32,370(0.9971)^x`

Answer 2

If the increase is x% per year, the multiplier each year is 1+x (expressed as a decimal).

Bozeman = 27,509·1.0196^t
Butte = 32,370·0.9971^t
where t is the number of years after 1990.