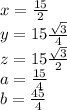Answer:
Here we have right triangles, which we can solve using trigonometric reasons, bceause we know the acute angles and the hypothenuse of the bigger right triangle.
Let's the sin function
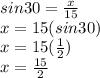
Then, we use the cosine function
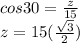
Now, we use the sin to find
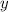 in the middle size right triangle
in the middle size right triangle
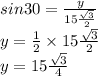
Then, we use cosine in the smaller triangle
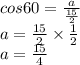
Also, we know that
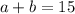 , and
, and
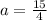 , so
, so
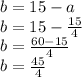
Therefore, all the answers are