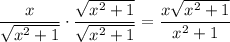Question

Trigonometric Identities PLEASE HELP

Answer 1

Suppose
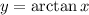
`y=\arctan x`, where
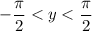
`-\frac\pi2<y<\frac\pi2`. The restriction on the domain of
`y` is needed for the following step; over this interval, we can properly take the inverse of
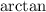
`\arctan`, i.e. take the tangent of both sides:



`y=\arctan x\iff\tan y=\tan(\arctan x)=x`


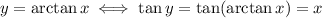
Just to emphasize the point, we can only simplify
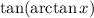
`\tan(\arctan x)` to
`x` as long as
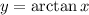
`y=\arctan x` is smaller than
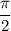
`\frac\pi2` in absolute value.


Now imagine you have a right triangle with a reference angle of
`y`. We're told that
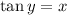
`\tan y=x`. In this triangle, then, the lengths of its legs occur in a ratio of
`\frac x1`. In other words, if one of the legs had length
`1` (the leg adjacent to the angle), then the other must have length
`x` (the leg opposite the angle).


By the Pythagorean theorem, it would follow that the length of the hypotenuse is
`√(x^2+1^2)=√(x^2+1)`. Then the sine of this angle is



`\sin(\arctan x)=\sin y=\frac x{√(x^2+1)}`

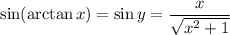
Personally, I wouldn't deem it necessary to rationalize the denominator, but we could go ahead and do it for giggles.


`\frac x{√(x^2+1)}\cdot(√(x^2+1))/(√(x^2+1))=(x√(x^2+1))/(x^2+1)`