We're given:
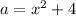
And with that we must rewrite the equation
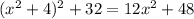
in terms of

.
Currently, the equation is written in terms of

, so lets start by writing

in terms of

:
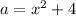

Now lets replace every

in
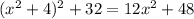
by
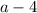
:
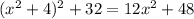
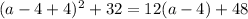
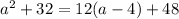
Now that we have the equation in terms of

, lets equal it to 0:
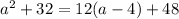

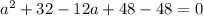
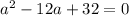
So the equation (in terms of

) is written in a standard form as
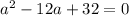
.
We can clearly see that the coefficient of

is -12 and the constant is 32.