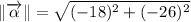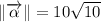Answer:
1a) a)
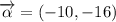 , 1b)
, 1b)
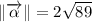 , 2a)
, 2a)
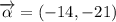 , 2b)
, 2b)
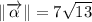 , 3a)
, 3a)
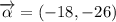 , 3b)
, 3b)
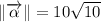
Explanation:
1a) The vectors
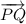 and
and
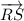 are determined:
are determined:
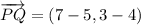
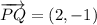
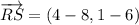
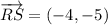
The component form of the resultant vector is:
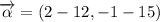
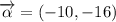
1b) The magnitude of the resultant vector is:
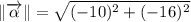
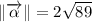
2a) The vectors
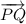 and
and
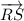 are determined:
are determined:
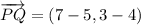
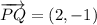
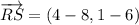
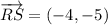
The component form of the resultant vector is:
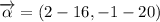
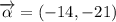
2b) The magnitude of the resultant vector is:
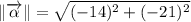
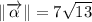
3a) The vectors
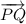 and
and
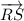 are determined:
are determined:
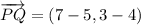
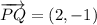
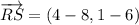
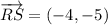
The component form of the resultant vector is:
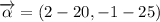
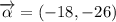
3b) The magnitude of the resultant vector is: