Question

Triangle XYZ has vertices X(–1, –1), Y(–2, 1), and Z(1, 2). What is the approximate measure of angle Z?

Answer 1

The answer to this question is A. 37.2°

Answer 2

37.9°

Explanation:

Notice that angle Z is formed by sides XZ and YZ.

First, we need to find the slopes of each side.

`m_(XZ)=(2-(-1))/(1-(-1))= (2+1)/(1+1)=(3)/(2)`

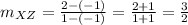
The slope of side XZ is 3/2.

`m_(YZ)=(2-1)/(1-(-2))=(1)/(1+2)=(1)/(3)`

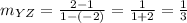
The slope of side YX is 1/3.

Now, we need to recur to the angle-slope formula, which is gonna give us the angle between both sides, that is, angle Z.

`tan(\angle Z)=|(m_(XZ)-m_(YZ))/(1+(m_(XZ))(m_(YZ))) |`

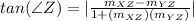
Replacing each slope, we have

`tan(\angle Z)=|((3)/(2)-(1)/(3) )/(1+(3)/(2)((1)/(3))) |\\tan(\angle Z)=|((9-2)/(6) )/(1+(1)/(2) ) |=|((7)/(6) )/((3)/(2) ) |\\tan(\angle Z)=|(14)/(18) |=|(7)/(9) |`

Then, we solve for
`\angle Z`

`\angle Z=tan^(-1)((7)/(9) ) \approx 37.9\°`

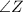
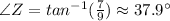
Therefore, the approximate measure of angle Z is 37.9°