Part A is accomplished by first factoring out the b^2 to get
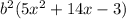
. Factor that completely using the quadratic formula to get
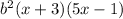
. Part B is done entirely with the quadratic formula (only cuz that's the easiest way to factor a second degree polynomial!) to get (x-9)(x-9) or (x-9) multiplicity 2. Part C is done by taking roots. Keep in mind that since this is a second degree polynomial you will have 2 solutions.
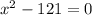
, therefore,
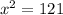
and
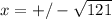
which is +11 and -11. And you're done! Factoring is very important...make sure you learn it and learn it well!!!