Question

The amount of money in an account with continuously compounded interest is given by the formula A = Pert , where P is the principal, r is the annual interest rate, and t is the time in years. Calculate to the nearest hundredth of a year how long it takes for an amount of money to double if interest is compounded continuously at 6.2%.

Answer 1

t = 11.2 yr

Explanation:

A = final value

P = initial value

r = rate

t = time

We are looking for the time and the equation that will be used is A = P
`e^(rt)`.

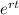We know that we are looking for how long it takes for an amount of money to double.

2P = P
`e^(0.062(t))` (the "P" cancels out)

= 2 =
`e^(0.062(t))`

= ln(2) = 0.062(t) (plug into a calculator)

= t = 11.2

Answer 2

Fill in the given values and solve for t.
2P = P*e^(.062t)
2 = e^(.062t)
ln(2) = .062t
ln(2)/.062 = t ≈ 11.18

It will take about 11.18 years for money to double at 6.2% when interest is compounded continuously.