Answer:
1.75927
Explanation:
Refer the attached figure
x y
0.4 2
0.9 2.4
1.5 2.6
2.2 3.1
2.6 3.5
3.3 3.8
Mean =
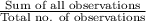
Mean of x values :

Mean of y values :
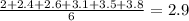
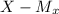
-1.4167
-0.9167
-0.3167
0.3833
0.7833
1.4833
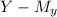
-0.9
-0.5
-0.3
0.2
0.6
0.9
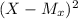
2.0069
0.8403
0.1003
0.1469
0.6136
2.2003
SS: 5.9083
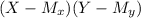
1.275
0.4583
0.095
0.0767
0.47
1.335
SP: 3.71
Sum of X = 10.9
Sum of Y = 17.4
Mean X = 1.8167
Mean Y = 2.9
Sum of squares (SS) = 5.9083
Sum of products (SP) = 3.71
Regression Equation = ŷ = bX + a
b = SP/SS = 3.71/5.91 = 0.62793
a =
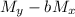 = 2.9 - (0.63*1.82) = 1.75927
= 2.9 - (0.63*1.82) = 1.75927
Thus ŷ = 0.62793X + 1.75927
Equation of line : y =mx+c
Where m = slope
c = y-intercept
Comparing regression equation with equation of line
ŷ = 0.62793X + 1.75927
m= 0.62793
y-intercept =1.75927
Hence the approximate y-intercept of the resulting regression line is 1.75927