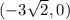Answer:
The equation of ellipse is given by:
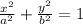 ....[1]
....[1]
where,
a and b are the semi major axis and semi minor axis.
Foci of ellipse =
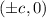
where,

As per the statement:
Given the ellipse is:
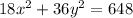
Divide both sides by 648 we have;
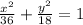
On comparing with [1] we have;
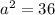 and
and
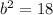
First find c:
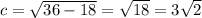
Foci of the ellipse are:
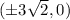
Therefore, the foci of the ellipse are,
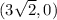 and
and