Question

(08.01, 08.02, 08.03, 08.05, 08.06 MC)

Part A: Factor x2a2 + 3xa2 + 2a2. Show your work. (4 points)

Part B: Factor x2 + 2x + 1. Show your work. (3 points)

Part C: Factor x2 − 1. Show your work. (3 points

Answer 1

For part A, the only thing you can do with those a^2 terms is factor one out of each expression leaving you with
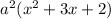
`a^(2) ( x^(2) +3x+2)`. You could further factor that quadratic to get
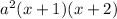
`a^(2) (x+1)(x+2)`. That is A factored completely. For B, this factors into (x+1) multiplicity 2, or
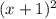
`(x+1) ^(2)`. Factor C by taking roots. Solve it for x by adding 1 to both sides and taking the square root of 1, both the principle and negative roots. Don't forget ever that the degree of the polynomial dictates how many roots or solutions you have. Here's C:
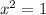
`x^(2) =1`, therefore,
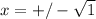
`x=+/- √(1)`. Since the square root of 1 is 1, your solutions are x = 1 andx = -1

Answer 2

You know that the product of two binomials can be written as
(x+a)(x+b) = x² + (a+b)x + ab
That is, the factors of the constant term (a and b) add up to give the coefficient of the linear term (a+b).

Part A.
The factor a² is immediately recognizable as a common factor. Removing that leaves the quadratic x²+3x+2. The factors of 2 (1 and 2) add to give 3 (the coefficient of x), so the complete factorization is
a²(x+1)(x+2)

Part B.
The factors of 1 (1 and 1) add to give 2 (the coefficient of x), so the factorizaton is
(x+1)(x+1) = (x+1)²

Part C.
The factorization of the difference of squares is a "special form" you will have memorized. It is the product of a sum and difference.
x²-1 = (x-1)(x+1)