Answer: The required slope-intercept f the line AB is
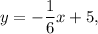
where
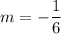 and c = 5.
and c = 5.
Step-by-step explanation: Given that a line AB passes through points A(–6, 6) and B(12, 3).
We are to find the equation of the line in slope-intercept form, y = mx + c.
The line AB passes through the points A(-6, 6) and B(12, 3), so the slope of the line AB will be
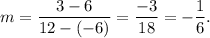
Also, since A(6, -6) is a point on the line AB, so the equation of the line is given by

Thus, the required slope-intercept f the line AB is
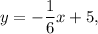
where
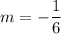 and c = 5.
and c = 5.