Question

Find the constant variation for xy=12

Answer 1

6 if that is an option

Answer 2

The expression given to us is:
`xy=12`

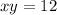
If we divide both sides by
`x` then the above expression can be rewritten as:

`y=(12)/(x)`

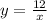
Now, we know that 12 is a constant, so the above equality can be changed into a proportionality as:

`y=(12)/(x)\Rightarrow y=12* (1)/(x)`

`\therefore y\propto(1)/(x)`

Thus, we now know that there is an inverse proportionality between
`y` and
`x` which has a constant of proportionality, also known as the constant of variation to be 12.