1. First, we are going to find the value of

form April. We know form our problem that
the maximum afternoon temperature in month, x, with x = 0 representing January, x = 1 representing February, and so on; therefore:
January

February

March

April
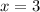
Now that we know that the value of
 that represent April is 3, we just need to replace
that represent April is 3, we just need to replace
 with 3 in our model and evaluate:
with 3 in our model and evaluate:
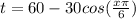
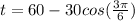
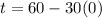

We can conclude that the maximum temperature in April will be 60.
2. Remember that in a function of the form
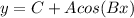
 is the amplitude
is the amplitude
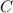 is the vertical shift
is the vertical shift
We have tow option to change our model to increase the maximum temperature to global warming:
1. Increase the value of D to increase the vertical shifting of the model. D affects the maximum value of the function; if we increase D, the maximum value of the function will increase as well. We know from our model that
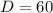 , so to increase the maximum temperature of our model, we just need to increase the value of 60.
, so to increase the maximum temperature of our model, we just need to increase the value of 60.
2. Increase the value of A to increase the amplitude of the model. The amplitude, also increases or decreases the maximum value of the function -regardless of the sing of A, so if we increase the value of A, we will increase the value of the function. We know from our model that
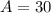 , so to increase the maximum temperature of our model, we just need to increase 30 (without considering the sign).
, so to increase the maximum temperature of our model, we just need to increase 30 (without considering the sign).