Question

Please someone help me with this question.

Answer 1

It's probably a little late here, but your sake later as for the sake of others, I'll get you through this. First thing to do is to convert that sin^2(2x) into something that is not a sin anymore, since the other 2 expressions are in cos. This problem is filled with trig identities and substitutions. Use the fact that sin^2(2x) = (2sin(x)cos(x))(2sin(x)cos(x)):
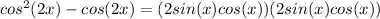
`cos ^(2) (2x)-cos(2x)=(2sin(x)cos(x))(2sin(x)cos(x))`. Simplify the right side to get:
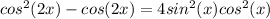
`cos ^(2) (2x)-cos(2x)=4sin ^(2)(x)cos ^(2)(x)`. Those 2 squared terms on the right have their own identities for substitution, so I'll fill them into the next equation:
`cos ^(2)(2x)-cos(2x)=4( (1-cos(2x))/(2) )( (1+cos(2x))/(2) )`. Now you'll FOIL out the right side to get rid of those parenthesis you worked so hard to get in there in the first place:
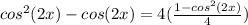
`cos ^(2) (2x)-cos(2x)=4( (1-cos ^(2)(2x) )/(4) )` and the 4's cancel out leaving you with
`cos ^(2)(2x)-cos(2x)=1-cos ^(2)(2x)`. Now get everything on the same side of the equation, combine like terms, and get ready to factor:
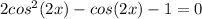
`2cos ^(2)(2x)-cos(2x)-1=0`. To save our sanity here, let's let u = cos(2x), so what we are actually factoring looks simpler:
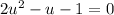
`2 u^(2)-u-1=0`. That factors nicely into u = 1 and u = -1/2. But you have to put your u equivalent back in in terms of the cos(2x):
`cos(2x)=1` and
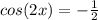
`cos(2x)=- (1)/(2)`. We still need one more identity here to make things easier and that is the fact that
`cos(2x)=2cos ^(2)(x)-1`. Sub that in for both equations we found:
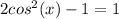
`2cos ^(2)(x)-1=1` and
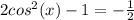
`2cos ^(2)(x)-1=- (1)/(2)`. Let's work on the first one of those first. Add 1 to both sides to get
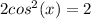
`2cos ^(2) (x)=2` and divide by 2 to get
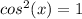
`cos ^(2)(x)=1` and
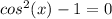
`cos ^(2)(x)-1=0`. This also factors because it is the difference of perfect squares: (cosx -1) = 0 and (cosx + 1) = 0. Solve each of those for cos(x) and get that cos(x) = 1 and cos(x) = -1. Save those for later and we'll use our unit circles to find all the solutions at one time. For the second equation, we have the same thing going on, Add 1 to both sides to get
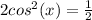
`2cos ^(2)(x)= (1)/(2)`. I multiplied both sides by 2 to get rid of the fraction on the right to get
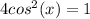
`4cos ^(2) (x)=1` then divided by 4 to get
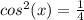
`cos ^(2) (x)= (1)/(4)`. This also factors out because of the difference of perfect squares into
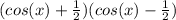
`(cos(x)+ (1)/(2) )(cos(x)- (1)/(2))`. Set each of these equal to 0 and then solve for cos(x) and you'll get
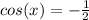
`cos(x)=- (1)/(2)` and
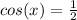
`cos(x)= (1)/(2)`. Now we're ready to look at our unit circle. We have 4 equations now: cos(x) = 1; cos(x) = -1; cos(x) = 1/2; cos(x) = -1/2. Find on the unit circle where cos is 1 and you'll get 0, 360; find where cos is -1 and you'll get 180; find where cos is 1/2 and you'll get 60 and 300; find where cos is -1/2 and you'll get 120 and 240. And you're finally done!! Phew! Get to know those trig identities. Us teachers do not give them to you to just annoy you...they're very important.