Question

The fish population of Lake Collins is decreasing at a rate of 3% per year. In 2004 there were about 1,300 fish. Write an exponential decay function to model this situation. Then find the population in 2010.

Answer 1

1083 fish

Explanation:

The fish population of Lake Collins is decreasing at a rate of 3% per year.

If starting population were about 1,300 in 2004 so the sequence will be

1,300, (1300 - 3% of 1300)..............

or 1300, 1261,.........

We know exponential function is modeled by

`A_(n) =A_(0) (r)^(n)`

Where
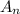`A_(n)` = population at time t.

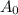`A_(0)` = initial population

r = common ratio

n = time in years.

Common ratio (r) =
`\frac{\text{second term}}{\text{first term}}`

=
`(1261)/(1300)=(0.97)`

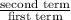
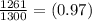
Then the function will be
`A_(n)=1300(0.97)^n`

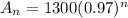
Then population in year 2010 (after 6 years) will be

`A_(6)=1300(0.97)^6`

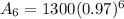
= 1300(0.8329)

= 1082.86 ≈ 1083 fishes

Answer 2

For this case we have a function of the form:

`y = A * (b) ^ x` Where,
A: initial amount
b: decrease rate
x: time in years
Substituting values we have:

`y = 1300 * (0.97) ^ x`
For 2010 we have:

`y = 1300 * (0.97) ^ 6 y = 1083`
Answer:
an exponential decay function to model this situation is:
y = 1300 * (0.97) ^ x
The population in 2010 is:
y = 1083