Question

A farmer wants to know which of two fertilizers will yield the most produce. He sets up twenty random plots of equal size on one acre. None of the plots are contiguous. He prepares the soil of all 20 plots identically except for the choice of fertilizer, using fertilizer Z on ten of the plots and Y on the other ten. He plants the same number of seeds from the same batch in all 20 plots. Throughout the growing season all 20 plots are maintained, watered, weeded, and treated exactly the same except that the ten plots that got fertilizer Z get only that same fertilizer. All the Y plots get only that fertilizer.

When the produce is ready for harvest, he tracks the yield for each plot in weight. The results are shown in the table.

Z Plots Y Plots
456 395
454 390
449 391
453 402
431 395
456 405
445 432
430 438
463 420
438 425


A. Calculate the mean for sample Z and for sample Y.
B. Which sample will have larger measures of deviation from the mean? In two or more complete sentences, explain your answer.

Answer 1

A) Calculate the mean for sample Z and for sample Y.

Z Plots Y Plots

456 395

454 390

449 391

453 402

431 395

456 405

445 432

430 438

463 420

438 425

`Mean = \frac{\text{Sum of all observations}}{\text{No. of observations}}`

`\text{Mean of sample Z}=(456+454+449+453+431+456+445+430+463+438)/(10)\\\\Mean=(4475)/(10)\\\\Mean=447.5`

`Mean\text{Mean of sample Y}=(395+390+391+402+395+405+432+438+420+425)/(10)\\\\\\Mean=(4093)/(10)\\\\Mean=409.3`

B)Since the observations of sample Y are more away from its mean as compared to Sample Z so, Sample Y will have larger measures of deviation from the mean

Answer 2

A)

Mean for:

Sample Z -- 447.5

Sample Y-- 409.3

B)

Sample Y has larger deviation from the mean.

Explanation:

Z Plots Y Plots

456 395

454 390

449 391

453 402

431 395

456 405

445 432

430 438

463 420

438 425

A)

For sample Z--

The mean is calculated by:

Ratio of sum of all the data points of Z-sample to the total number of points i.e. 10.

`Mean=(456+454+449+453+431+456+445+430+463+438)/(10)\\\\Mean=(4475)/(10)\\\\Mean=447.5`

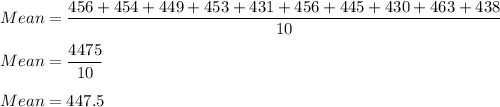
Similarly for sample Y--

The mean is calculated as follows:

`Mean=(395+390+391+402+395+405+432+438+420+425)/(10)\\\\\\Mean=(4093)/(10)\\\\Mean=409.3`

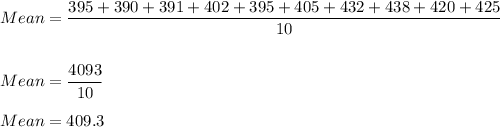
B)

As we could see that the data Y has a greater spread from the mean as compared to the sample Z.

As all the points in the sample Z are close to the mean and have less spread.

The standard deviation is most commonly used to measure the spread of the data.

Standard deviation of sample Z is: 10.651

Standard deviation of sample Y is: 16.9944

Hence Sample Y have larger deviation from the mean.