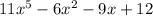Question

Which polynomial is in standard form? A) 26x^5+12x^7-8x^3+6x

B) 3x^5+x-6x^2+5
C) 11x^5-6x^2-9x+12
D) 5x^2+18x^2-12x^4+4x^7
PLEASE HELP!!!!

Answer 1

It's C. In order to be in standard form you have to have all your exponents in descending order. They don't all have to be there in order, the ones that are just have to go from highest to lowest.

Answer 2

Option C -
`11x^5-6x^2-9x+12`

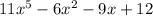
Explanation:

To find : Which polynomial is in standard form?

Solution :

The standard form of a polynomial is defined as each term in order of degree is written from highest to lowest.

The degree is the power of a variable.

Now, we check the order of each polynomial.

A)
`26x^5+12x^7-8x^3+6x`

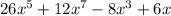
The degree of the polynomial is 5,7,3,1 not from highest to lowest.

So, No the polynomial is not in standard form.

B)
`3x^5+x-6x^2+5`

The degree of the polynomial is 5,1,2 not from highest to lowest.

So, No the polynomial is not in standard form.

C)
`11x^5-6x^2-9x+12`

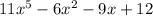
The degree of the polynomial is 5,2,1 is from highest to lowest.

So, Yes the polynomial is in standard form.

D)
`5x^2+18x^2-12x^4+4x^7`

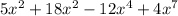
The degree of the polynomial is 2,2,4,7 not from highest to lowest.

So, No the polynomial is not in standard form.

Therefore, Option C is correct.

The standard form of the polynomial is
`11x^5-6x^2-9x+12`