Question

The function y = x 2 - 10x + 31 has a ____

value of ____.

options for the first blank -
A. maximum
B. minimum
options for the second blank -
A. 31
B. 10
C. 6
D. 5

Answer 1

Option B. minimum is correct for the first blank

Option C. 6 is correct for second blank.

Explanation:

In order to find the maxima or minima of a function, we have to take the first derivative and then put it equal to zero to find the critical values.

Given function is:

`f(x) = x^2-10x+31`

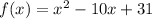
Taking first derivative

`f'(x) = 2x-10`

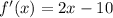
Now the first derivative has to be put equal to zero to find the critical value

`2x-10 = 0\\2x = 10\\x = (10)/(2) = 5`

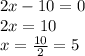
The function has only one critical value which is 5.

Taking 2nd derivative

`f''(x) =2`

`f''(5) = 2`

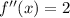
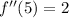
As the value of 2nd derivative is positive for the critical value 5, this means that the function has a minimum value at x = 5

The value can be found out by putting x=5 in the function

`f(5) = (5)^2-10(5)+31\\=25-50+31\\=6`

Hence,

The function y = x 2 - 10x + 31 has a minimum value of 6

Hence,

Option B. minimum is correct for the first blank

Option C. 6 is correct for second blank.