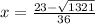Your question isn't quite formatted correctly to be a quadratic equation as it has no variable for the "a" and "b" terms but I'll just insert them and hopefully it will match what you're asking.
Let x be our variable.
36x² - 46x - 22
The quadratic formula for a quadratic equation in the format ax² + bx + c = 0 is:
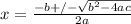
Now we just insert our terms to the formula:

And now we solve:
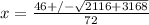

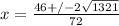
Your final answers when you simplify:
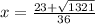
and