Question

A stone is thrown straight down from a tall building. The relation h = 150 - 5t - 5t^2

approximates its path, with h in metres and t in seconds.
a) How tall is the building?
b) Factor the right side of the equation fully.
c) When does the stone hit the ground?

Answer 1

a) The building is 150 m tall

b) h(t)=-5(t+6)(t-5)

c) The stone hits the ground at 5 seconds.

Explanation:

Function Models

The path of a stone thrown down from a tall building is modeled by the function:

`h(t)=150-5t-5t^2`

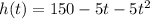
Where h is the height in meters and t is the time in seconds after the stone is thrown.

a) To find the height of the building, we set t=0 because it's the moment when the stone is thrown and has the same height as the building:

`h(0)=150-5*0-5*0^2`

`h(0)=150`

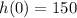
The building is 150 m tall

b) The function is

`h(t)=150-5t-5t^2`

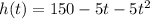
Factoring out -5:

`h(t)=-5(-30+t+t^2)`

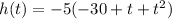
Rearranging:

`h(t)=-5(t^2+t-30)`

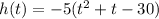
To factor the polynomial in parentheses, we must find two numbers whose product is -30 and sum is 1. We can also use the quadratic formula to find the roots and factor later.

These numbers are 6 and -5, thus the function is:

`h(t)=-5(t+6)(t-5)`

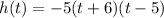
c) The stone hits the ground when h=0:

`-5(t+6)(t-5)=0`

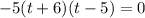
The equation has two solutions:

t = -6

t = 5

The only feasible solution is t = 5, thus the stone hits the ground at 5 seconds.