Answer:
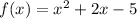
Explanation:
We need to find the function
 representing a quadratic function.
representing a quadratic function.
Now, we know that the general form of a quadratic function is
 , where
, where
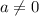
So, Let us consider each function one by one.
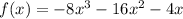
Clearly, the above function has a cubic term in it so it is a cubic function NOT a quadratic function.
Now,
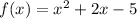
Clearly, the above function is of the form
 so, it is a quadratic function.
so, it is a quadratic function.
Now,
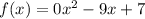
Here, the coefficient of
 is 0. So, it is not of the form
is 0. So, it is not of the form
 , where
, where
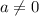 .
.
So, it is NOT a quadratic function.
Hence, only
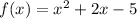 is a quadratic function among the all functions.
is a quadratic function among the all functions.