Question

Explain one of the theorems that you would use to find the zero of higher degree polynomial

Answer 1

Rational Root Theorem:

If the rational number
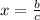`x=(b)/(c)` is a zero of a higher degree polynomial:

`P(x)=kx^(n)+...+m`

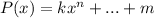
where all the coefficients are integers. Then
`b` will be a factor of
`m` and
`c` will be a factor of
`k`

1. Use the rational root theorem to enumerate all possible rational zeroes of the polynomial
`P(x)`

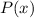
2. Evaluate the polynomial from the first step until you can find a zero. Let’s suppose the zero is
`x=r`. It will be a zero if
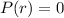`P(r)=0`. Then if this is true, write the polynomial as:

`P(x)=(x-r)Q(x)`

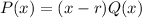
3. Repeat this process using
`Q(x)` this time rather than
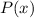`P(x)`. The process finishes until we reach a second degree polynomial, then solve as it is widely known for a quadratic equation.