Answer with explanation:
→→The equation of curve 1 ,which is in the shape of parabola is ,when represented in general form
![y= -2x^2-4 x + 12\\\\ y=-2[x^2+2 x-6]\\\\ (y)/(-2)=(x+1)^2-6-1\\\\ (-y)/(2)+7=(x+1)^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/k0wu6np7satbmhhflireve2i72bvlo330a.png)
So, Coordinate of vertex can be obtained by
→ x+1=0
x= -1
and,
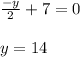
is equal to , (-1,14).
x-Coordinate of vertex of the function ,
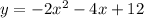 is equal to -1.
is equal to -1.
→→→The equation of curve 2 ,which is in the shape of parabola is ,when represented in general form
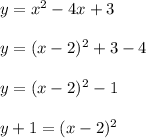
So, Coordinate of vertex can be obtained by
→ x-2=0
x= 2
and, →y+1=0
y= -1
is equal to , (2,-1).
x-Coordinate of vertex of the function ,
 is equal to 2.
is equal to 2.