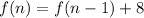Question

Suppose the 4th term of an arithmetic sequence is 27, and the 8th term

is 59.
1. What are the first term and the common difference?
2. Write a function for the sequence.

Answer 1

The first term is 3 and common difference is 8.

And

The formula for sequence is:
`a_n = -5+8n`

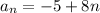
Function is:
`f(n) = f(n-1)+8`

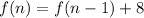
Explanation:

Given that

`a_4 = 27\\a_8 = 59`

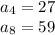
The general formula for arithmetic sequence is:

`a_n = a+(n-1)d`

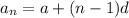
Here

a is the first term

n is the term number

and d is the common difference

for 4th term

`a_4 = a+(4-1)d\\27 = a+3d\ \ \ Eqn\ 1`

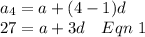
For 8th term

`59 = a+ (8-1)d\\59= a+7d\ \ \ \ \ Eqn\ 2`

subtracting equation 1 from equation 2

`59-27 = a+7d-(a+3d)\\32 = a+7d-a-3d\\32 = 4d\\d =(32)/(4)\\d = 8`

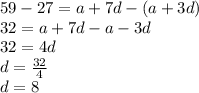
Putting d = 8 in equation 1

`a+3d = 27\\a+3(8) = 27\\a+24=27\\a = 27-24\\a = 3`

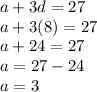
Now for the function

`a_n = a+(n-1)d\\a_n = 3+(n-1)(8)\\a_n = 3 + 8n-8\\a_n = -5+8n`

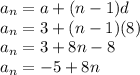
The sequence can also be expressed as a function as:

`f(n) = f(n-1) + 8`

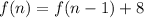
Hence,

The first term is 3 and common difference is 8.

And

The formula for sequence is:
`a_n = -5+8n`

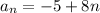
Function is:
`f(n) = f(n-1)+8`