Answer: The required value of x is - 2.
Step-by-step explanation: We are given the following two functions :

We are to find the value of x for which (f + g)(x) = 0.
We know that for any two functions p(x) and q(x), the following property holds true :
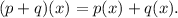
We have
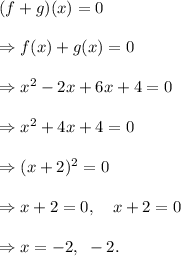
Thus, the required value of x is - 2.