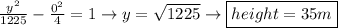The graph of the path of the swooping bird is shown in figure below. The general form of the hyperbola equation is given by:
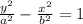
So we can order the equation of the problem by multiplying it by the following term:
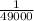
Therefore:
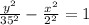
∴
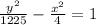
Given that the origin lies at ground level, t
he bird is closest to the ground at the vertices of the parable, that is, when x = 0 (this will give us two solutions, but we will take the positive value because the bird flight over the air)