Question

What are the explicit equation and domain for a geometric sequence with a first term of 2 and a second term of −8?

an = 2(−8)n − 1; all integers where n ≥ 1
an = 2(−8)n − 1; all integers where n ≥ 0
an = 2(−4)n − 1; all integers where n ≥ 0
an = 2(−4)n − 1; all integers where n ≥ 1

Answer 1

Hi,
Answer is D.


`a_1=2\\ a_2=-8=a_1*r\Rightarrow\ r= (-8)/(2) =-4\\ a_2=2*(-4)\\ a_3=2*(-4)^2\\ \boxed{a_n=2*(-4)^(n-1)\ for\ n \geq 1} \\`

Answer 2

The answer is option 4

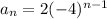`a_n=2(-4)^(n-1)`; all integers where n ≥ 1

Explanation:

Given the first term and second term of geometric sequence.

we have to find the explicit equation and domain for a geometric sequence.

The formula for nth term of G.P is

`a_n=ar^(n-1)`

`a=2, a_2=-8`

`a_2=ar^(2-1)`

`-8=2r`

`r=-4`

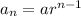
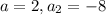
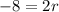
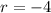
Hence, the explicit equation becomes

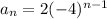`a_n=2(-4)^(n-1)`; all integers where n ≥ 1

Option 4 is correct.