Question

A car driving 22.7 m/s on flat ground drives off a 42.3 m high cliff. How much time does it take to reach the ground?

Answer 1

Answer:2.94

Explanation: It’s correct.

Answer 2

We are only concerned about the vertical motion of the car, since we want to know how much time it takes to reach the bottom of the cliff, 42.3 meters below. Calling h=42.3 m, the vertical position of the car at time t is given by:

`y(t)=h +v_(0y) t- (1)/(2)gt^2`
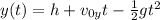
where
`g=9.81 m/s^2` is the gravitational acceleration, and
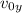
`v_(0y)` is the initial vertical velocity of the car, which is zero since the car is initially travelling only in the horizontal direction. Therefore, the equation becomes

`y(t)=h- (1)/(2)gt^2`
We want to find the time t at which y(t)=0, so we have

`t= \sqrt{ (2h)/(g) }= \sqrt{ (2(42.3 m))/(9.81 m/s^2) }=2.9 s`
The car takes 2.9 seconds to reach the ground.