We have to functions, namely:
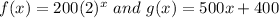
So the problem is asking for the smallest positive integer for

so that

is greater than the value of
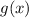
, that is:
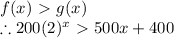
Let's solve this problem by using the trial and error method:
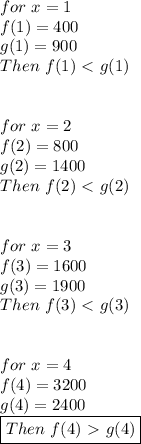
So starting

from 1 and increasing it in steps of one we find that:
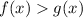
when
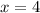
That is,
the smallest positive integer for

so that the function

is greater than
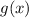 is 4.
is 4.