Question

What are the zeros of the function f(x)=x2−5x−24 ? enter your answers in the boxes. the zeros of f(x) are and ?

Answer 1

`f(x)=x^2-5x-24\\\\x^2-5x-24=0\\\\x^2+3x-8x-24=0\\\\x(x+3)-8(x+3)=0\\\\(x+3)(x-8)=0\iff x+3=0\ \vee\ x-8=0\\\\\boxed{x=-3\ \vee\ x=8}`

Answer 2

The zeros of any equation lie on the x axis.On x axis y=0.The zeros can be found by substituting y=0 and finding the corresponding y values.

The given equation is :

`y=x^(2)-5x-24`

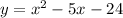
Comparing it with quadratic equation
`y=ax^(2)+bx+c`

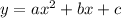
We have a=1,b=-5,c=-24.

To find the zeros we substitute y=0.

`x^(2)-5x-24=0.`

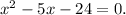
WE need to find two numbers which on multiplication will give us ac that is 1(-24)=-24.The same numbers on addition should give us b=-5.

The two numbers are -8 and 3.-8 times 3=-24 and -8+3=-5.

The factors of the equation are (x+8)(x-3)=0

making both factors =0 we have:

x+8=0 and x-3=0

Solving for x

x=-8 and x=3.

The two zeros of the equation are -3,8.