These are difficult. You'll have 3 equations with 3 unknowns in the end to solve in order to get the coefficients right. The standard form for a circle with this type of info is
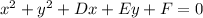
. We have 3 points with different x and y coordinates that we will sub in to get these 3 equations we seek. First point (29, 1):
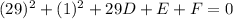
. This simplifies down to 842+29D + E + F =0. That's the first of 3 equations. Next point (-19, 1):
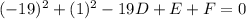
which simplifies down to 362-19D+E+F=0. That's the second equation. Last point (-2, 18):

. Which simplifies down to 328-2D+18E+F=0. That's the 3rd equation. In all of these move the constants over to the other side of the equals sign. 29D+E+F= -842; -19D+E+F= -362; -2D+18E+F= -328. Take the first 2 equations and solve for D. Do this multiplying one of them by -1 to get a set of equations that are 29D+E+F= -842 and 19D-E-F= 362. Solve this by elimination and the E and the F cancel each other out leaving you with 48D= -480 and D = -10. Now take the second 2 equations and sub in the value for D you just found and work on eliminating either E or F. -19(-10) +E+F= -362 which simplifies to 190+E+F= -362; -2(-10)+18E+F= -328 simplifies to 20+18E+F= -328. Move the constants from the left to the right by subtraction to get a set of equations that is E+F= -552 and 18E+F= -348.Solve that first equation for E: E=-552-F and sub it into the second equatiion. 18(-552-F)+F= -348 and F= -564. Now let's go back to E+F= -552 and sub in our F of -564 to find that E = 12. Therefore, our equation, when all is said and done an hour later, is
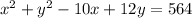
. Not sure if that's the form your teacher wants it in, but that's standard. Ugh.