Question

tim has a large collection of books. the number of paperback books he owns is three less than four times the number of hardcover books, in total tim had 447 books how many hardcover books does he own

Answer 1

tim has 90 hardcover books

Explanation:

Answer 2

We can solve this by setting up a couple of equations.

Let's allow x to represent the number of paperbacks Tim owns, and allow y to represent the number of hardcover books he owns.

Using the information in the question, we can write the equations:

1)
`x = 4y-3`
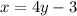
2)
`x+y=447`

Let's rearrange equation 1 so that it is in standard form:


`x-4y=-3`

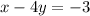
And then let's multiply equation 2 by 4 so that we can cancel out y when we solve the system of equations:


`4(x+y=447)`

`4x+4y=1,788`

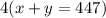
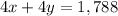
Then we can add the two equations and solve for x:

1)
`x-4y=-3`
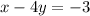
+ 2)
`4x+4y=1,788`
------------------------------------

`5x=1,785`


`x=357`

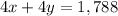
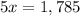
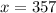
So now we now the number of paperback books Tim has is 357. Let's plug this into one of the original equations to solve for the number of hardcover books (y):


`357+y=447`

`y=90`

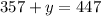
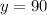
And now we know that Tim owns 90 hardcover books.