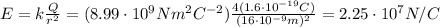If the atom of carbon has lost 4 electrons, it has now an excess of charge equal to +4e:
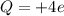
where
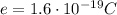
Its charge is concentrated in the nucleus, so we can treat it as a single-point charge, whose electric field is given by:
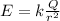
where k is the Coulomb's constant and r is the distance from the charge. In our problem,
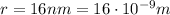
therefore the electric field at this distance is