Answer:
Question 27
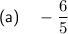
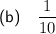
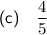
Question 28

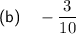
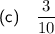
Explanation:
The gradient of a straight line can be found by dividing the difference in the y-coordinates by the difference in the x-coordinates between two points on the line.
A positive gradient slopes up from left to right.
A negative gradient slopes down from left to right.

We can use the formula to find the gradients, or we can simply calculate the change in y and change in x by looking at the graph.
Example:
If we take line (a) from question 27 as an example.
- The change in y from the beginning to the end of the line is 6 units.
- The change in x from the beginning to the end of the line is 5 units.
- The line slopes down, so the gradient is negative.
Therefore, the gradient is -6/5.
Using the gradient formula, define two points on the line:
- Let (x₁, y₁) = (0, 6)
- Let (x₂, y₂) = (5, 0)
Input the points into the formula:
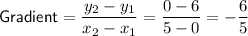
Solutions
Question 27
(a) The gradient is -6/5, as calculated above.
(b) The change in y is 1 unit and the change in x is 10 units. The line slopes up so the gradient is positive. Therefore, the gradient is 1/10.
(c) The change in y is 4 units and the change in x is 5 units. The line slopes up so the gradient is positive. Therefore, the gradient is 4/5.
Question 28
(a) The change in y is 6 units and the change in x is 0 units. Therefore, the gradient is undefined since anything divided by 0 is undefined. Therefore, this line has no gradient.
(b) The change in y is 3 units and the change in x is 10 units. The line slopes down so the gradient is negative. Therefore, the gradient is -3/10.
(c) The change in y is 3 units and the change in x is 10 units. The line slopes up so the gradient is positive. Therefore, the gradient is 3/10.
Attachment
I have marked the change in y (green) and the change in x (blue) for line (c) on both graphs.