2 Answers

Agirault · Answer 1 · 2019-09-02T12:30:53+0000

So first we need to find the slope. The equation find slope is:

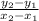
( y_(2) -y_(1) )/( x_(2)- x_(1) )

Either of the points could be denoted as '1' or '2',

Let's plug in the point (0, 8) as '1' and (-1, 10) as '2':

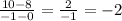
(10-8)/(-1-0) = (2)/(-1)=-2

So we know that the slope, m, is equal to -2.

The point-slope equation is:

y- y_(1)=m(x- x_(1))

where m is the slope and
x_(1)

and

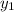
are the point. So since we have two points here, we can pick one to use for the equation. Let's use (-1, 10):

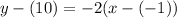
y-(10)=-2(x-(-1))

**We need to make sure that we have accounted for all of the signs. Remember that two negatives equal a positive:

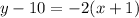
y-10=-2(x+1)

And there is your point slope form of the line that passes through the two points.

Please log in or register to add a comment.