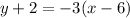Question

Find the Point-Slope equation of the line containing the given point and having the given slope. (6, -2), m = -3

Answer 1

So we know that the Point-Slope equation is as follows:


`y- y_(1)=m(x- x_(1))`

where m is the slope, and
`x_(1)` and
`y_(1)` are the point. So let's plug those numbers in now:


`y-(-2)=-3(x-(6))`

**We need to make sure that we do these signs correctly. Remember that two negatives equal a positive. Let's simplify:


`y+2=-3(x-6)`

And this is now your equation in Point-Slope form!

Answer 2

`y+2=-3(x-6)`

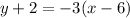
Explanation:

Pre-Solving

We are given that a line has a slope (m) of -3, and passes through the point (6, -2).

We want to write the equation of this line in point-slope form, which is
`y-y_1=m(x-x_1)`, where m is the slope and
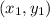`(x_1,y_1)` is a point, hence the name.

Solving

As we are already given the point and the slope, we can use their values to find the equation.

Starting with the slope, substitute m with -3.

`y-y_1=-3(x-x_1)`

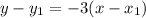
Now, replace
`x_1` with 6 and
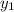`y_1` with -2. Remember that the formula has subtraction.

So, we get:

`y--2=-3(x-6)`

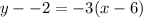
This can be simplified to:

`y+2=-3(x-6)`