Question

The smallest integer that can be added to -2m^3-m+m^2+1 to make it completely divisible by m+1 is

Answer 1

We can use the polynomial remainder theorem here.
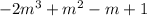
`-2m^3+m^2-m+1` will be exactly divisible by
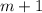
`m+1` if the remainder upon division of it by
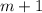
`m+1` is 0. The PRT says that this remainder is exactly equal to the value of the polynomial when
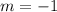
`m=-1`. We have


`-2(-1)^3+(-1)^2-(-1)+1=5`

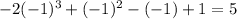
Since the remainder is 5, that's how much we should subtract from the original polynomial. So the integer that we need to add is -5.

To confirm: by the PRT, the remainder should be 0. We get


`-2(-1)^3+(-1)^2-(-1)+1-5=0`