Question

What are the minimum, first quartile, median, third quartile, and maximum of the data set? 45, 76, 12, 39, 87, 65, 23, 32

a.
min=12
max=87
1st Q=70.5
3rd Q=27.5
median=42

b.
min=12
max=87
1st Q=27.5
3rd Q=70.5
median=42

c.
min=12
max=87
1st Q=27.5
3rd Q=76
median=45

d.
min=12
max=87
1st Q=23
3rd Q=76
median=42

Answer 1

The minimum is 12
The maximum is 87
The median is 42
The first quartile is 27.5
The third quartile is 70.5
The answer will be
B.

Answer 2

The correct option is b.

Explanation:

The given data set is

45, 76, 12, 39, 87, 65, 23, 32

Arrange the data in ascending order.

12, 23, 32, 39, 45, 65, 76, 87

The minimum value of the data is 12 and the maximum value of the data is 87.

Divide the data in two equal parts.

(12, 23, 32, 39), (45, 65, 76, 87)

Median divides the data in two equal parts. So, the midpoint of 39 and 45 is median.

`Median=(39+45)/(2)=42`

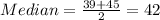
Divide each parenthesis in two equal parts. First quartile divides the first parenthesis in two equal parts and third quartile divides the second parenthesis in two equal parts.

(12, 23), (32, 39), (45, 65), (76, 87)

`Q_1=(23+32)/(2)=27.5`

`Q_3=(65+76)/(2)=70.5`

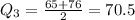
First quartile is 27.5, third quartile is 70.5 and median is 42. Therefore the correct option is b.